未经组委会书面许可，请勿转载。

2018年全国大学生数学建模竞赛论文C101.pdf

大型百货商场会员画像描述

摘 要

当前电商的发展使商场会员不断流失，给零售运营商带来了严重损失，在大数据时代，完善“会员画像”描绘，通过数据挖掘，加强对现有会员的精细化管理，实施会员细分和精准营销，不仅能够维系会员的忠诚度，给商场带来更大的利润，还能够节约商场的营销成本。

针对问题一，借助 SQL Server 数据库的储存与处理功能，先把数据导入 SQLServer 数据库，然后根据单据号提取需要的特征数据，即分别提取出会员与非会员的消费数据（见附录 1），再导入 excel 统计出会员的消费金额、购买数量及购买商品的平均价格，非会员的消费金额、购买数量及购买商品的平均价格；最后列表对比会员与非会员群体的差异及会员群体给商场带来的价值（见表4-4）。

针对问题二，本题选用 K-均值聚类法，以消费金额和消费次数作为衡量会员购买力的特征数据，运用 SPSS 软件对提取好的数据（见附录 2）对会员进行聚类，K 值以公式（1）进行确定。D=类内平均距离/类间平均距离 （1），K 取4 使 D 值最小，故将会员分为四类：大众会员（45678 人）、黄金会员（2708 人）、铂金会员（348 人）和砖石会员（17 人），其中各类别中心点见表 4-6。

针对问题三，我们自定义规则：我们选择最近没有消费行为天数和消费次数，作为划分会员生命周期阶段的指标，把会员生命周期划分为五个阶段：引入期- 成长期-成熟期-休眠期-流失期，选择 2015 年 1 月 1 日至 2018 年 1 月 3 日范围内登记的会员作为研究对象，分析其生命周期和活跃状态。利用附件 1 与附件 3的数据，通过 SQL Server 及 excel 统计出会员的周期阶段以及状态划分，具体见附录 3. 针对问题四，重新定义：会员当月有消费记录则当月为活跃状态，否则当月为非活跃状态。取登记时间为 2015 年到 2016 年共 13671 个会员为研究对象，根据其消费明细统计得到 2017 年活跃状态矩阵（见表 4-9）。基于活跃状态矩阵采用 matlab 计算其马尔科夫状态转移矩阵（见表 4-10），由表 4-10 可知，在2017 年，会员整体从非活跃到活跃的激活率为 7.46%；根据销量数据分析，激活率与销售量的相关系数为 0.83，即激活率与促销活动成强线性相关关系，通过线性拟合（见图 4-4）可得销售量与激活率的关系表达式为一元二次方程: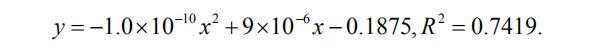 

针对问题五，根据著名的“尿布与啤酒的故事”，本题对相关数据进行关联规则挖掘，采用 FP-Growth 算法(python 代码见附录 5.2）对会员消费明细数据进行关联分析。首先根据会员卡号+消费时间+商品编码删除一次消费中商品重复数据，然后根据会员卡号+消费时间提取每次购物篮商品数据，最后采用购物篮数据进行关联规则分析，支持度计数设为 50，即规则支持度计数大于等于 50 才是频繁项集，算法计算结果如置信度等见表附录 5.1。通过关联分析给出促销建议：（1）将置信度高的 X 和 Y 商品摆放在相同区域，以便会员能同时找到这几种商品，很快完成购物。（2）适当降低置信度高的 X 商品价格，会促进 Y 商品的连带销售。（3）置信度建议选取 0.8 及以上。