机场航班延误问题的建模与分析
苏同发,王肖,李梦
(华北电力大学(保定),河北保定,071000)
摘 要
本文主要研究国内机场航班延误的相关问题,首先对国际上航班延误最严重的10个机场进行排名,分析我国机场航班在其中的排名情况。然后找出影响国内航班延误的主要因素,最后针对航班延误主要因素提出有效改进措施,并分析改进措施对航班延迟的改进效果。
针对问题一,本文采用聚类分析改进的AHP模型对全球主要机场进行分析,得到延误最严重的机场排名,与题目相比分析可得,题目中的结果与所得的结果并不相符,因此得到题目所述不准确的结论。本模型首先依据延迟程度不同作为准则层进行打分,并通过聚类分析淘汰偏离统一标准的机场机构意见,进而得到各准则的评判权重,再计算出加权总延迟率得到具体排名。
针对问题二,本文首先通过Excel对所得数据进行可视化分析,初步得到影响航班延误的主要原因是航空公司,其次为天气和流量。然后建立了主成分回归模型对数据进行定量分析,依据主成分分析得到影响航班延误的三个主成分因子,再通过EViews软件对因子进行最小二乘法(OLS)估计,代换得回归表达式,进而发现结果与上述相同。
针对问题三,本文决定根据第二问的结果对航空公司和流量管制两个可控方面进行改进。对于流量管制方面,主要针对飞机跑道终端区建立了自适应遗传排队模型,以北京首都机场为例,进行三跑道十五架飞机同时降落优化,并将结果与现有的FCFS算法相比较,进一步说明本模型的优越性。
其次,针对航空公司方面原因,本文主要针对机场机位的健壮性进行了优化以减少延误的连带效应。据此建立了机位分配健壮模型,首先得到两个航空公司延时概率分布,然后以总的机位冲突概率最小为目标函数建立不同航班的规划方程,通过贪婪算法初步得到局部最优结果,再通过禁忌搜索对初步结果进一步优化,得到最终的机位分配。
在最后,把难以实现的求解过程复杂度降低,与其他算法进行了比较,对模型进行了评价和推广,即灵敏度分析,使其能更好的应用于实际生产生活中。
关键词:聚类分析层次分析法 主成分分析最小二乘估计遗传算法禁忌搜索
目 录
一.问题重述........................................................ 1
二.问题分析........................................................ 1
2.1.对问题一的分析................................................. 1
2.2.对问题二的分析................................................. 2
2.3.对问题三的分析................................................. 3
三.模型假设........................................................ 3
四.符号说明........................................................ 3
五.问题一的模型的建立与求解........................................ 5
5.1.数据预处理..................................................... 5
5.2.计算平均延迟率................................................. 5
5.3 模型的建立—聚类分析的改进AHP模型............................. 5
六.问题二的模型建立和求解......................................... 10
6.1 模型建立的准备—机场航班数分析................................ 10
6.2 模型的建立—主成分回归模型.................................... 12
七.问题三模型的建立和求解......................................... 16
7.1 模型建立准备.................................................. 16
7.2 模型一的建立—遗传算法终端区排队模型.......................... 16
7.3 模型二的建立—机位分配健壮模型................................ 24
7.4 灵敏度分析.................................................... 31
八.模型优缺点..................................................... 32
8.1.优点.......................................................... 32
8.2.缺点.......................................................... 32
8.3模型推广....................................................... 32
九.参考文献...................................................... 32
一.问题重述
一项跟踪世界各地空中旅行情况的报告显示,就航班准时起飞和抵达而言,中国内地机场和航空公司的表现最差。香港南华早报网根据flightstats.com 的统计称:中国的航班延误最严重,国际上航班延误最严重的10个机场中,中国占了7个。其中包括上海浦东、上海虹桥、北京国际、杭州萧山、广州白云、深圳宝安、成都双流等机场。
根据我国国内的延迟率统计标准,将延迟的航班分为准点、略晚点、较晚点、严重晚点。如果一个航班在计划到港时间后30min内完成着陆(机轮接地),即认为该航班准点到港,30-45min为略晚点,45-60min为较晚点,60min则为严重晚点。
附件一列出了以我国延迟率统计为标准的2014年6月-2015年3月全球主要机场准点率。附件二、三列出了2010-2014年我国延误航班数目和各个原因所占比例。
现要求通过数学建模来完成以下任务:
(1) 分析附件1中2014年6月-2015年4月全球主要机场的准点率报告,制定评判延误程度的规则,根据计算出的结果与香港南华早报网的统计结果是否相符从而得出结论是否正确。
(2) 在问题一得出的中国各大机场延迟程度的基础上,结合附件2中的国内民航统计数据,建立航班延迟评价体系,确定影响我国航班延误的主要原因。
(3)综合附件一、二资料,从影响我国航班延误的主要原因出发,确定改善我国航班延误的主要措施。
根据问题初步分析可知,需要建立模型确定全球各大机场的延迟严重程度,并找出导致国内机场延迟的主要原因,设计改进措施。在模型建立过程中,还需要充分考虑机场承载量,当地天气原因,旅客需求量,突发事件和航空管制使模型更加具体且贴近实际。
二.问题分析
2.1.对问题一的分析
分析2014年6月-2015年4月全球主要机场的准点率报告[2],制定评判延误程度的规则,分析通过计算出的结果与香港南华早报网的统计结果是否相符得出结论是否正确。
首先用Excel软件中的数据分析工具对国际各大机场的样本量进行筛选,剔除了样本量较小的中小型机场。筛选出了排名前60的国际主要机场。
然后根据已有数据确定判断机场航班延迟严重性排名的标准。机场的略晚点、较晚点、严重晚点航班占总航班数的比率都是判断机场延迟严重程度的直接标准。而纵向比较发现一般情况下,各大机场样本量和准点率不成相关性。由于国际各大机场承载量和调节能力存在显著差异,在机场自身可调节承载量范围内,机场样本量的增加不会使机场准点率的下降。由于各大机场规模大小不一,其对应承载量存在较大差异。所以不将机场样本量作为判断机场延迟严重程度的标准。从而确定判断机场严重程度的标准为略晚点率、较晚点率、严重晚点率。
接着应用一种聚类分析的层次分析法思想,确定略晚点、较晚点、严重晚点这三个指标权重。首先应用层次分析法让多家航空机构对三个指标进行打分的,然后通过聚类分析思想,对三个指标权重进行合理的修正以弱化主观因素的影响,最后根据最终权重进行60个国际主要机场的延迟严重程度的排名,并与题目给出的全球排名前十的中国七大机场进行比较,得出结论是否正确。
2.2.对问题二的分析
分析附件二2010-2013年民航行业发展统计公报和附件三2009-2014年从统计看民航的原始数据进行统计,得到2019-2013年我国国内主要机场每年总航班数、不正常航班数目和各延误因素导致的不正常航班数。然后我们做出国内主要机场的不正常航班数随年份变化趋势和各延迟因素导致航班延迟数随年份的变化趋势的直方图,以年份进行纵向比较,用直方图直观分析我国近几年来不正常航班数变化趋势和各延迟因素因素对其的影响强度。再做出每年航班延误各个因素所占比例的饼状图,横向比较各航班延迟因素在当年度所占比例,直观观察各航班延迟因素的影响程度。
建立主成分回归模型,以各机场延迟因素导致航班延迟数为自变量,航班总延迟数为因变量来构造原始变量的线性组合,得到一组能含有绝大部分的原始变量信息的新变量,解决原始变量多重线性问题。将得到的新变量作为自变量进行线性回归分析,使用EViews软件进行最小二乘法(OLS)估计。然后原始变量代回新变量,通过对航班各个延迟因素对总不正常航班数的影响系数的分析来确定影响我国航班延误的主要原因。
2.3.对问题三的分析
影响我国航班延误的的因素按照可控与否,可分为不可控因素和可控因素,其中可控因素是航班延误研究和治理的重点。根据第二问的结论,影响我国航班延误的主要原因是航空公司、流量管制和天气。为了更好的处理有天气等不可控因素引起的航班延误,做好相应的延误补救措施,减少由不可控因素引发的航空公司、流量管制等可控因素引起的起飞延误、到达延误以及由此引发的延误波及效应,可以建立遗传算法终端区排队模型,通过优化进场飞机排序来达到优化终端区流量管理的目的。减少因排队等待的时间,降低航空公司调配强度。对于航空公司方面主要影响因素为机位的分配问题,主要分析两个航空公司在同一机场航班存在的冲突概率,建立机位分配健壮模型,采用贪婪算法进行初步冲突局部优化,最后采用禁忌搜索确定冲突概率最小的全局最优解。
三.模型假设
(1)假设收集到的数据都是真实可靠的;
(2)假设国际上各航空公司对航班延误的定义是一样的;
(3)假设我们考虑到的航班延误因素是全面的;
(4)假设航班延误因素对航班延误的影响都是独立的;
(5)假设飞机在起飞降落过程中没有非正常事故发生;
(6)假设飞机都是按照预计是时间到达进行排队。
四.符号说明
符号 含义
![]() 权重矩阵
权重矩阵
![]() 第
第![]() 个因素的权重
个因素的权重
![]() 机构
机构![]() 与机构
与机构![]() 权重结果的相似程度
权重结果的相似程度
![]() 机构意见偏离程度
机构意见偏离程度
![]()
![]() 的特征值
的特征值
![]()
![]() 的特征向量
的特征向量 ![]() 向量
向量![]() 的第
的第![]() 个分量
个分量
符号 含义
![]() 第
第![]() 主成分
主成分
![]() 交叉概率
交叉概率
![]() 变异概率
变异概率
![]() 前机和后机之间的最小尾流间隔标准
前机和后机之间的最小尾流间隔标准
![]() 第
第![]() 架飞机预定到达跑道的时间
架飞机预定到达跑道的时间
![]() 第
第![]() 架飞机的排序到达时间
架飞机的排序到达时间
![]() 适应度函数
适应度函数
![]() 最小尾流间隔标准
最小尾流间隔标准
![]() 需要指派机位的航班数量
需要指派机位的航班数量
![]() 机场可用的机位数量
机场可用的机位数量
![]() 航班i的计划到港时间
航班i的计划到港时间
![]() 航班j的计划离港时间
航班j的计划离港时间
![]() 机位k的开始可用时间
机位k的开始可用时间
![]() 机位k的机位类型
机位k的机位类型
![]() 航空公司A、B航班的最大提前到港时间
航空公司A、B航班的最大提前到港时间
![]() 航空公司A,B航班的最大延误
航空公司A,B航班的最大延误
![]() 0-1决策变量
0-1决策变量
![]() 航班
航班![]() 在机位k发生机位使用冲突的概率
在机位k发生机位使用冲突的概率
![]() 航班
航班![]() 和航班j在时间范围
和航班j在时间范围![]()
内占用机位k的概率
![]() 总的航班机位冲突概率
总的航班机位冲突概率
五.问题一的模型的建立与求解
5.1.数据预处理
全球机场数据庞大,不同月份各大机场的准点率存在差异,处理起来极其费力,而华南早报中Flightstasts网站是对全球主要国际机场的航班延迟情况的分析,所以我们首先对所得样本进行筛选,比较全球大中型机场的航班延迟情况。
对于一个航空公司,其样本量为实际起飞、到达或取消记录的航班量。先根据全球机场2014年6月-2015年3月的准点率报告进行全球主要国际机场的筛选,剔除样本量相对较小的国际小型机场,筛选出样本数排名前六十的国际主要大中型机场进行下一步准点率的比较。
5.2.计算平均延迟率
机场航班延迟程度随月份波动严重,经过分析发现与机场当月样本量成正相关。所以应采取计算出机场每月不同程度的延机数进行累加除以机场每月样本量之和的方法确定机场航班平均延迟率。由于全球机场2014年6月-2015年3月的准点率报告中对于一些机场准点率报道数据不充足,则对于机场统计遗漏的月份采用全部月份求和取平均来填补此遗漏月份延迟数据。采用这两种方法来减少由于特定月份对于机场延迟程度的影响。
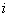 (1)
(1)
5.3 模型的建立—聚类分析的改进AHP模型
5.3.1 改进的聚类分析AHP方法的原理
应用层次分析法[4]确定机构给定的指标权重,将定性分析和定量分析相结合,弱化主观因素的影响。并且通过聚类分析方法[1],通过机构数标准或偏离程度标准设定的闲值淘汰某个或某些机构的意见,对多个机构所分配的权重进行修正,使机构意见筛选更为科学,从而得到了群体机构对该评价指标的最后权重最并且给出决策结果。
5.3.2 模型求解
(1)建立层次结构模型
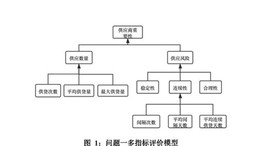
将决策问题分解为三个层次,最上层为目标层,即机场延迟程度排名,最下层为方案层,为经过筛选出的![]() 60个国际主要大型机场。中间层为准则层,由略延迟、较延迟、严重延迟三个评价指标组成。各层间的联系用相连的直线表示如图一所示。(图中准则层和方案层的连线从略)。
60个国际主要大型机场。中间层为准则层,由略延迟、较延迟、严重延迟三个评价指标组成。各层间的联系用相连的直线表示如图一所示。(图中准则层和方案层的连线从略)。
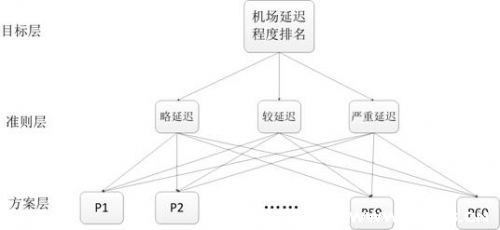
图1:层次分析法三层结构模型
(2)确定判断矩阵
方案层对准则层的权重已经在附录1全球机场2014年6月-2015年3月的准点率报告中给出。下面进行准则层(延迟程度)对目标层(延迟严重性排名)影响的打分确定准则层对目标层的权重。
根据已有数据挑选10个有代表性的机场机构,应用1-9尺度评价标准,对略晚点、较晚点、严重晚点三种延迟程度进行两两比较打分。建立10个判断矩阵。
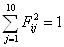
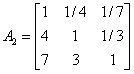
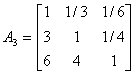
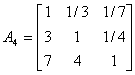
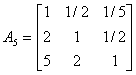
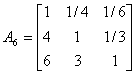
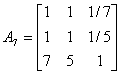
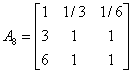
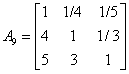
(3)计算权向量并做一致性检验:
![]() (2)
(2)
求解判断矩阵![]() 的最大特征值
的最大特征值![]() ,再根据公式(2)最大特征值求出对应的特征向量
,再根据公式(2)最大特征值求出对应的特征向量![]() ,并将
,并将![]() 标准化,即为同一层相对于上一层某一因素的权重,根据此权重的大小,便可确定该层因素的排序。
标准化,即为同一层相对于上一层某一因素的权重,根据此权重的大小,便可确定该层因素的排序。
![]() (3)
(3)
![]() (4)
(4)
取一致性指标![]() (
(![]() 为
为![]() 的阶数),取随机性指标
的阶数),取随机性指标![]() ,若通过公式(4)则认为
,若通过公式(4)则认为![]() 具有一致性。否则需要对判断矩阵
具有一致性。否则需要对判断矩阵![]() 进行调整,直到具有满意的一致性为止。
进行调整,直到具有满意的一致性为止。
一致性检验结果:
表1 一致性检验结果
![]()
![]() 是否通过一致性检验
是否通过一致性检验
3.0385 0.0332 是
3.0324 0.0279 是
3.0536 0.0462 是
3.0324 0.0279 是
3.0055 0.0048 是
3.0536 0.0462 是
3.0126 0.0109 是
3.0536 0.0462 是
3.0858 0.0739 是
3.0536 0.0462 是
打分矩阵![]() 通过一致性检验。
通过一致性检验。
经过计算得到十个机构权重系数:
表2 十个机构权重系数
权重\延迟程度 略延迟 较延迟 严重延迟
![]() 0.104729 0.258285 0.636986
0.104729 0.258285 0.636986
![]() 0.078617 0.262753 0.658630
0.078617 0.262753 0.658630
![]() 0.091402 0.217638 0.690959
0.091402 0.217638 0.690959
![]() 0.084144 0.210920 0.704936
0.084144 0.210920 0.704936
![]() 0.128271 0.276350 0.595379
0.128271 0.276350 0.595379
![]() 0.085220 0.270557 0.644223
0.085220 0.270557 0.644223
权重\延迟程度 略延迟 较延迟 严重延迟
![]() 0.108472 0.261434 0.630093
0.108472 0.261434 0.630093
![]() 0.104800 0.396120 0.49908
0.104800 0.396120 0.49908
![]() 0.101323 0.255317 0.643360
0.101323 0.255317 0.643360
![]() 0.067933 0.161755 0.770312
0.067933 0.161755 0.770312
(4)建立评价因素权重集
设评价因素权重集为10个机构对略延迟,较延迟和严重延迟程度的权重系数。
用层次分析法求出评价指标的权重集![]() ,
,![]() 是第
是第![]() 个机构的对第
个机构的对第![]() 个因素的评价权重,且满足
个因素的评价权重,且满足![]() 。
。
(4)修正评价因素的权重
如果用层次分析法处理后得出来的权重矩阵如下:

矩阵系数指第![]() 个机构对第
个机构对第![]() 个指标判断后经层次分析法处理后得到的权重和重要程度。
个指标判断后经层次分析法处理后得到的权重和重要程度。
为了判断矩阵中各机构所得权重的离散程度,需要计算各权重间的相似系数并由此组成相似系数矩阵。相似系数![]() 和相似系数矩阵
和相似系数矩阵![]() 如下:
如下:
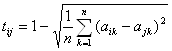 (5)
(5)
其中![]() 指机构
指机构![]() 与机构
与机构![]() 权重结果的相似程度,
权重结果的相似程度,![]() 越小,则相似程度越小。
越小,则相似程度越小。![]() 表示指标权重的维数,即所评价指标的个数。
表示指标权重的维数,即所评价指标的个数。![]() 表示机构意见的总数,即参加权重评估的机构总人数。显然,
表示机构意见的总数,即参加权重评估的机构总人数。显然,![]() 。
。
十个机构的相似系数矩阵:
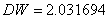
![]() (6)
(6)
其中![]() 表示相似系数的矩阵中第
表示相似系数的矩阵中第![]() 行之和,它表示第
行之和,它表示第![]() 个机构判断得出的权重意见与其他机构群体(包括他自己)评估所得权重意见的偏离程度。相似系数之和越小,则机构意见距离其它机构意见越远,偏离程度越大。
个机构判断得出的权重意见与其他机构群体(包括他自己)评估所得权重意见的偏离程度。相似系数之和越小,则机构意见距离其它机构意见越远,偏离程度越大。![]() 表示相似系数对行求和形成的一列。
表示相似系数对行求和形成的一列。
得到十个机构的偏离程度:
![]()
剔除离异程度大的权重,本文根据专家淘汰比率标准来剔除离异程度大的权重。在剔除权重过程中,淘汰专家太多,就失去了群体决策评价的作用;淘汰专家太少,则又使个别与群体评价权重偏离程度大的专家影响评价结果。根据评价经验,应用聚类分析法淘汰专家的比例在20%~30%为好,具体如表所示:
表3 专家淘汰比率标准
聘请专家人数 5 6 7 8 9 10
聚类分析淘汰人数 1 1-2 1-2 2 2-3 2-3
采用意见的专家人数 4 4-5 5-6 6 6-7 7-8
根据表1专家淘汰比率标准,可排除机构八、机构与十给出的权重,排除后剩下的权重求平均值,得到修正之后的权重:
![]()
5.3.3模型结果
根据修正之后的权重![]() 与附录一中方案层(六十个国际主要机场)对准则层各个延迟程度的百分比
与附录一中方案层(六十个国际主要机场)对准则层各个延迟程度的百分比![]() 综合比较,计算出国际主要机场的加权总延迟率
综合比较,计算出国际主要机场的加权总延迟率![]() ,得出机场的最终排名:
,得出机场的最终排名:
![]() (7)
(7)
表4 国际主要机场延迟严重性排名
排名 机场名称 加权总延迟率
1 杭州萧山 0.1770386
2 上海浦东 0.1656947
3 上海虹桥 0.1598703
4 深圳宝安 0.1500059
5 广州白云 0.1379725
6 芝加哥奥黑尔 0.1279817
7 纽约拉瓜迪亚 0.1257216
8 西安咸阳 0.1233421
9 费城 0.1173728
10 重庆江北 0.1154537
11 北京国际 0.1072205
12 成都双流 0.1002741
5.3.4结果分析
根据在聚类分析的改进AHP方法计算了符合群体决策评价的新的年度机场延迟率。并对全球主要60名机场的排名,可以得到国际上航班延误最严重的10个机场中有7家中国机场,它们分别是:杭州萧山、上海浦东、上海虹桥、深圳宝安、广州白云、西安咸阳、重庆江北。与香港南华早报网给出的7家延误最严重的中国机场相比有差异。西安咸阳和重庆江北代替北京国际和成都双流位列全球延误最严重航班前十名。在聚类分析的改进AHP方法的分析下北京国际和成都双流排在国际航班延误最严重机场的第11和12名。
总体来说,同国际机场延误水平相比,我国机场航班延误最严重。
六.问题二的模型建立和求解
6.1 模型建立的准备—机场航班数分析
我国航班延误原因分为11类:天气、公司、流量、机场、联检、油料、离港系统、旅客、军事活动、公共安全和空管[6-9]。因由空管导致航班延迟数每年为个位数,对总不正常航班影响可忽略不计。
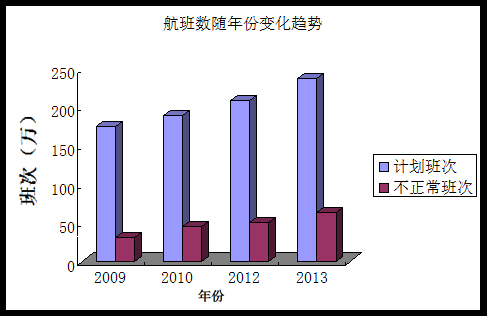
图2:航班数随年份变化趋势
图2是我国2009年到2013年度航班数的发展情况,以及不正常航班数的变化趋势,初步分析,随着我国经济发展,飞机作为一种交通工具越来越普遍,人们对飞机作为交通工具的需求的增加引起国内航班数的逐年增加,也引起了带来了航班延误不正常班次的逐年增加,这需要我们分析导致机场航班延误的主要原因来对机场进行进一步的合理规划。
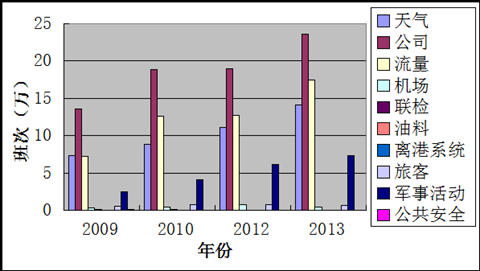
图3:各因素航班延迟数随年份变化趋势
根据我国近几年来各年度航班延迟因素所占比例的饼状图,横向比较各航班延迟因素在当年度所占比例,直观观察各航班延迟因素的影响程度。
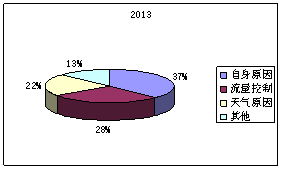 |
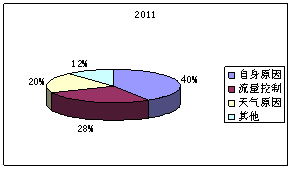
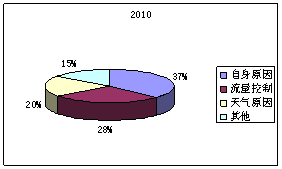
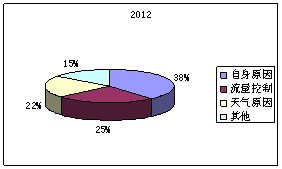 图4:2010年各延迟因素占不正常航班比例 图5:2011年各延迟因素占不正常航班比例
图4:2010年各延迟因素占不正常航班比例 图5:2011年各延迟因素占不正常航班比例
图6:2012年各延迟因素占不正常航班比例 图7:2013年各延迟因素占不正常航班比例
根据2010、2011、2012、2013年度延迟因素占不正常航班比例可以直观看出航班延误原因中航空公司自身原因、天气原因、和流量管制这三者所占延迟影响程度最大,而其他原因所占比重比较小。在这三者比较重,航空公司自身原因造成的延迟影响比重最大,而流量管制次之,三者相比天气原因所占延迟最小。
6.2 模型的建立—主成分回归模型
在本问题中,根据我国国内民航规定研究影响机场航班延迟的主要因素,建立主成分回归模型所选用的因变量是延迟航班数,自变量分别是:
(1)公司![]() ;(2) 天气
;(2) 天气![]() ;(3) 流量
;(3) 流量![]() ;(4) 机场
;(4) 机场![]() ;(5) 联检
;(5) 联检![]() ;(6) 油料
;(6) 油料![]() ;(7) 离港系统
;(7) 离港系统![]() ;(8) 旅客
;(8) 旅客![]() ;(9) 军事活动
;(9) 军事活动![]() ;(10) 公共安全
;(10) 公共安全![]() 。
。
表5 2009-2013年度各延迟因素导致航班延迟数
因素\年度 2009 2010 2012 2013
天气 49687 88966 111236 140958
公司 70891 188194 190060 236122
流量 45412 126064 126841 174882
机场 3308 4936 7831 4339
联检 1309 892 463 698
油料 4 26 15 11
离港系统 33 105 47 29
旅客 4448 7225 8133 6341
军事活动 25041 40828 61703 73060
公共安全 2393 235 119 484
6.2.1 主成分回归模型原理
主成分分析[10]通过构造原始变量的线性组合,得到一组的能反映原始变量绝大部分信息的新变量。从中挑出的几个新的变量含有尽可能多原始变量的信息,然后将其作为自变量,进行回归分析。可以在解决原始变量多重共线性问题的同时保持了原始变量的大部分信息。
6.2.2 模型建立
(1) 计算各年度10个延迟因素导致航班延迟数的相关系数矩阵![]() :
:
 (8)
(8)
相关系数矩阵为:

(2) 计算特征值、主成分贡献率和累计贡献率
计算特征值:
解特征方程![]() ,求出特征值
,求出特征值![]() ,并使其按大小顺序排列,即
,并使其按大小顺序排列,即![]() ;
;
计算主成分贡献率及累计贡献率:
根据特征值计算主成分![]() 的贡献率和累计贡献率,选择10个主分量
的贡献率和累计贡献率,选择10个主分量![]() ,一般取累计贡献率达85%-95%的特征值
,一般取累计贡献率达85%-95%的特征值![]() 所对应的第一,第二,…,第
所对应的第一,第二,…,第![]() 个主成分,说明前
个主成分,说明前![]() 个主成分
个主成分![]() 来描述样本所包含的信息已经达到要求。
来描述样本所包含的信息已经达到要求。
主成分![]() 的贡献率为:
的贡献率为:
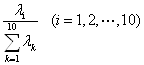 (9)
(9)
累计贡献率:
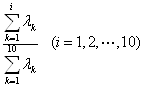 (10)
(10)
表6 特征值及主成分贡献率
主成分 特征值 贡献率 累计贡献率
天气 6.021 0.6021 0.6021
公司 2.7257 0.2726 0.8747
流量 1.2534 0.1253 1.0000
机场 0.0000 0.0000 1.0000
联检 0.0000 0.0000 1.0000
油料 0.0000 0.0000 1.0000
离港系统 0.0000 0.0000 1.0000
旅客 0.0000 0.0000 1.0000
军事活动 0.0000 0.0000 1.0000
公共安全 0.0000 0.0000 1.0000
由表6的特征值及主成分贡献率中可以看到,第一主成分![]() 的特征值
的特征值![]() 为6.021,能够解释总变异的60.21%,第二主成分
为6.021,能够解释总变异的60.21%,第二主成分![]() 的特征值
的特征值![]() 为2.7257,解释了总变异的27.26%,第三主成分
为2.7257,解释了总变异的27.26%,第三主成分![]() 的特征值
的特征值![]() 为1.2534,解释了总变异的12.53%。可知第一、第二、第三主成分的累计贡献率已近似100%,故需求出第一、第二、第三主成分
为1.2534,解释了总变异的12.53%。可知第一、第二、第三主成分的累计贡献率已近似100%,故需求出第一、第二、第三主成分![]() 即可。
即可。
(2)计算特征向量:
分别求出对应于特征值![]() 的特征向量
的特征向量![]() 。这里要求
。这里要求![]() ,即
,即![]() ,其中
,其中![]() 表示向量
表示向量![]() 的第
的第![]() 个分量。
个分量。
表7 主成分对应特征向量
因素\主成分 ![]()
![]()
![]()
天气 0.4176 0.662 -0.564
公司 0.6004 -0.3432 0.0697
流量 0.6114 -0.3828 -0.0241
机场 0.0051 0.0678 0.3694
联检 -0.0038 -0.0085 -0.0498
油料 0 -0.0006 0.001
离港系统 -0.0002 -0.0024 0.0026
旅客 0.008 -0.0008 0.2678
军事活动 0.302 0.5409 0.6736
公共安全 -0.0068 0.0129 -0.1096
从表7主成分载荷可以得到,第一主成分![]() 在天气、公司自身、流量管制上有相对极大的正载荷,它衡量了饼状图直观分析中航班延误主要因素,可称
在天气、公司自身、流量管制上有相对极大的正载荷,它衡量了饼状图直观分析中航班延误主要因素,可称![]() 为主要因素增长因子;第二主成分
为主要因素增长因子;第二主成分![]() 在天气军事因素这些不可控制的因素上有较大的负载荷,称
在天气军事因素这些不可控制的因素上有较大的负载荷,称![]() 为不可控增长因子;第三主成分
为不可控增长因子;第三主成分![]() 在机场旅客军事活动这些社会因素上有相对大的负载荷,故称
在机场旅客军事活动这些社会因素上有相对大的负载荷,故称![]() 为社会增长因子。
为社会增长因子。
6.2.3 模型结果
使用EViews软件将各个主成分![]() 当作自变量,延迟航班数
当作自变量,延迟航班数![]() 作为因变量,进行最小二乘法(OLS)估计:
作为因变量,进行最小二乘法(OLS)估计:
![]()
![]()
由![]() 可知,表达式
可知,表达式![]() 含有数据中的几乎全部的信息。
含有数据中的几乎全部的信息。
有![]() 一般性判断标准可知,
一般性判断标准可知,![]() 通过一般性,延迟航班数
通过一般性,延迟航班数![]() 与第一、二和三主成分
与第一、二和三主成分![]() 的关系符合一般性。
的关系符合一般性。
将![]() 分别用
分别用![]() 代换,得到总延迟航班数关于各个指标的回归表达式为:
代换,得到总延迟航班数关于各个指标的回归表达式为:
![]() 6.2.4 结果分析
6.2.4 结果分析
通过分析总延迟航班数![]() 关于各个指标的回归表达式,比较航班各个延迟因素对总不正常航班数的影响系数可知,天气、公司、流量这三个延迟因子前的影响系数显著高于其他延迟因子。总延迟航班数与公司因素正相关,即公司影响航班因子每增加1个单位,总航班延迟数就增加0.686994个单位。流量因素对航班总延迟有正向作用,流量因子每提高一个单位,航班总延迟就增加0.606732个单位。天气因素对航班总延迟的正影响为,天气因子每升高一个单位,总延迟就增加0.568375个单位。就为相比于其他航班延迟延迟因素。这三个主要延迟因子进行影响系数比较可知,航空公司因素对航班延迟程度最大,流量次之,天气在三者中印象程度最小。
关于各个指标的回归表达式,比较航班各个延迟因素对总不正常航班数的影响系数可知,天气、公司、流量这三个延迟因子前的影响系数显著高于其他延迟因子。总延迟航班数与公司因素正相关,即公司影响航班因子每增加1个单位,总航班延迟数就增加0.686994个单位。流量因素对航班总延迟有正向作用,流量因子每提高一个单位,航班总延迟就增加0.606732个单位。天气因素对航班总延迟的正影响为,天气因子每升高一个单位,总延迟就增加0.568375个单位。就为相比于其他航班延迟延迟因素。这三个主要延迟因子进行影响系数比较可知,航空公司因素对航班延迟程度最大,流量次之,天气在三者中印象程度最小。
并且利用主成分回归模型得出的我国航班延误的主要原因结论与通过Excel对所得数据进行可视化分析得出结果相同。
七.问题三模型的建立和求解
7.1 模型建立准备
根据第二问的结论得出影响我国航班延误的主要原因是航空公司、流量管制和天气。为了更好的改善我国航班延误,减少由可控因素直接影响航班延迟和由天气等不可控因素引起的航班延误,做好相应的延误补救措施,减少由不可控因素引发的航空公司、流量管制等可控因素引起延误波及效应。建立遗传算法终端区排队模型[5]有效减少由于多架飞机预计同时到达机场时造成的航班延误引起的延误波及所造成的流量管制和航空公司调配问题。
7.2 模型一的建立—遗传算法终端区排队模型
7.2.1 遗传算法
Ⅰ.基因和染色体
基因:跑道和飞机的个体
染色体:飞机基因和跑道基因组成的序列
Ⅱ.适应度
适应度是在研究自然界中生物的遗传和进化现象时,用来度量某个物种对于生存环境的适应程度。适应度高的物种获得更多的繁殖机会,反之则相对较少,甚至灭绝。
本模型采用飞机到达时间总延迟加1后的倒数作为适应度衡量值。
Ⅲ.选择
选择是指决定以一定的概率从中种群选择若干的个体的操作。一般而言,选择过程是一种基于适应度的优胜劣汰的过程。
本模型选择过程将采用基于适应度选择的轮盘赌算法实现。
Ⅳ.交叉
有性生殖生物在繁殖下一代时2个同源染色体之间通过交叉而重组,即在2个染色体的某一相同位置处DNA被切断,其前后2串分别交叉组合形成2个新的染色体。
本模型中交叉时,对选中的2条跑道染色体进行交叉操作,按照一定的交叉概率进行单点交叉。
Ⅴ.变异
在细胞进行复制时可能以很小的概率产生某些复制差错,从而使染色体发生某种变异,产生出新的染色体,这些新的染色体将表现出新的性状。
本模型中的变异采用对染色体中的飞机序列和跑道编号按照一定的变异概率进行变异。
Ⅵ.轮盘赌选择方法
适应度大的个体被选中的机会多,适应度小的个体被选中几率小,产生的结果是优胜劣汰。个体适应度按照比例转化为选中概率,将轮盘分成10个扇区,因为要进行10次选择,所以产生10个![]() 之间的随机数,相当于转动10次轮盘,获得10次轮盘停止时指针的位置,指针停在某一扇区,该扇区代表的个体即被选中。
之间的随机数,相当于转动10次轮盘,获得10次轮盘停止时指针的位置,指针停在某一扇区,该扇区代表的个体即被选中。
Ⅶ.单点交叉
单点交叉中,交叉点K的范围为![]() ,
,![]() 为个体变量数目,在该点分界相互交换变量。
为个体变量数目,在该点分界相互交换变量。
Ⅷ.自适应遗传算法
基本遗传算法中的交叉和变异概率是固定的,但是造成遗传算法性能不稳定,需要对其进行改进。
本模型采用自适应法对种群进行交叉和变异操作,交叉概率![]() 和变异概率
和变异概率![]() 能够随适应度自动改变。当种群各个体适应度趋于一致或者局部最优时,使
能够随适应度自动改变。当种群各个体适应度趋于一致或者局部最优时,使![]() 和
和![]() 增加;而当群体适应度比较分散时,使
增加;而当群体适应度比较分散时,使![]() 和
和![]() 减小。同时对于适应度高于群体平均适应值得个体,使该解得以保护,进入下一代;而低于平均适应值的个体,对应于较低的
减小。同时对于适应度高于群体平均适应值得个体,使该解得以保护,进入下一代;而低于平均适应值的个体,对应于较低的![]() 和
和![]() ,使该解被淘汰。因此,自适应的
,使该解被淘汰。因此,自适应的![]() 和
和![]() 能够提供相对某个解的最佳
能够提供相对某个解的最佳![]() 和
和![]() 。自适应遗传算法在保持种群多样性的同时,保证了遗传算法的收敛性。
。自适应遗传算法在保持种群多样性的同时,保证了遗传算法的收敛性。
自适应遗传算法中,![]() 和
和![]() 按照如下同时进行自适应调整
按照如下同时进行自适应调整
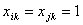 (12)
(12)
式中:![]() 为要交叉的2个个体中较大的适应值;
为要交叉的2个个体中较大的适应值;![]() 为每代群体的平均适应度值;
为每代群体的平均适应度值;![]() 为群体中最大的适应度值;
为群体中最大的适应度值;![]() 为要变异个体的适应度。
为要变异个体的适应度。
一般取![]() 。
。
7.2.2遗传算法终端区排队模型的原理
遗传算法从一组随机产生的初始航班和跑道开始搜索,在后代迭代中不断进化。在每一代中用适应值来衡量染色体(飞机基因和跑道基因组成的序列)的好坏,生成下一代飞机基因和跑道基因组成的序列,成为后代。后代是由前一代染色体通过交叉变异运算形成的。在新一代形成中,根据适应值的大小选择部分后代,淘汰部分后代,从而保持航班和跑道的大小为常数,适应值高的染色体被选中的概率较高。这样经过若干代只有,算法收敛于最好的飞机基因和跑道组成的序列,它就可能是问题的最后结或者次优解。
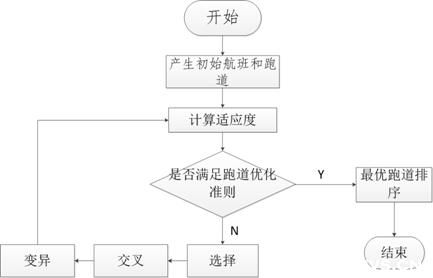
图8:遗传算法终端区排队模型流程图
7.2.3 模型建立
(1)定义染色体
模型中两条染色体分别代表飞机序列和跑道序列。一对染色体即决定了跑道分配和机场的排序、调度。对15驾飞机进行排序,每条染色体即包含15个基因。飞机序列染色体决定了飞机之间的相对位置,只有两家飞机位于同一跑道上他们之间的相对次序才是最重要的。对飞机进行排序后他们之间的间隔要满足最小尾流间隔,即
![]() (13)
(13)
式中:![]() 为前机和后机之间的最小尾流间隔标准;
为前机和后机之间的最小尾流间隔标准;![]() 为第
为第![]() 架飞机预定到达跑道的时间;
架飞机预定到达跑道的时间;![]() 为第
为第![]() 架飞机的排序到达时间。
架飞机的排序到达时间。
(2)遗传算法仿真
本模型以15架飞机,3条跑道为例进行仿真,15架飞机的航班代码分别为:
表8 15架飞机航班代码
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
HC1 | HC2 | HC3 | SC4 | HC5 | LC6 | HC7 | HC8 | HC9 | SC10 |
11 | 12 | 13 | 14 | 15 |
|
|
|
|
|
LC11 | HC12 | HC13 | LC14 | SC15 |
|
|
|
|
|
其中第一个字母表示飞机的类型,根据国际民航组织的规定,有三种类型飞机,分别是重型(H)、大型(L)、小型(S)。
飞机排序到达时间S不能早于相应的E(包含飞机性能和飞行模式的约束条件,具有通用性)。
飞机延迟定义为S和飞机到达2条跑道较早的E之间的差值:
![]() (14)
(14)
式(14)中:下标1、2分别表示1号跑道和2号跑道。
目标函数为延迟最小,所以适应度函数为:
![]() (15)
(15)
相应的飞机到达跑道E由一个![]() 的矩阵来表示,E的转置矩阵为:
的矩阵来表示,E的转置矩阵为:
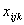
其中第一行表示15架同时预计降落的航班到达跑道1的时间,第二行表示到达2号跑道的时间,第三行表示到达3号跑道的时间。
不同类型飞机之间的最小尾流间隔标准由一个![]() 的时间矩阵来表示:
的时间矩阵来表示:
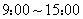
其中行代表前机,列代表后机,行和列代表的飞机种类依次是H、L、S。
(3)算法流程
1.目标函数为总的飞机延误时间加1的倒数,优化准则为当世代数超过预先设定值时,结束计算。
2.随机产生100个个体作为初始种群。
3.采用轮盘赌法对初始种群进行选择操作,适应值大的个体被选中,适应值小的个体被淘汰。
4.对跑道染色体进行交叉操作,按照式中计算交叉概率,采用单点交叉方法,如:
跑道染色体分别为:

随机选中第12位置为交叉点,进行交叉后,2条染色体分别为
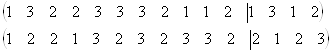
对飞机染色体进行变异操作,按照式中计算变异概率,进行变异操作时,随机选取飞机染色体中的两个基因进行互换,如飞机染色体为(数字代表飞机代码)
![]()
随机选中的基因为4和6两个位置,则变异之后的飞机染色体数即为:
![]()
(4)参数设置
本模型对遗传算法进行了改进,采用自适应的交叉和变异概率,取值分别按照式子计算的到。本模型遗传算法参数取为:染色体长度为15;种群大小为100;最大进化代数为100.
7.2.4 模型结果
根据先到先服务原则,按照飞机E的次序分配跑道和排序,仿真得到的排序结果如表9所示。
适应值趋于平稳状态得到的一对染色体如表10所示。
采用遗传算法进行航班终端排序所得结果如表11所示。
表9 飞机簇先到先服务仿真结果
1号跑道 | 2号跑道 | 3号跑道 | |||||||||
航班代号 | S | Emin | 延迟时间 | 航班代号 | S | Emin | 延迟时间 | 航班代号 | S | Emin | 延迟时间 |
HC2 | 6 | 6 | 0 | HC5 | 6 | 6 | 0 | HC13 | 6 | 6 | 0 |
HC3 | 7 | 6 | 1 | HC9 | 7 | 6 | 1 | LC6 | 13 | 13 | 0 |
HC7 | 8 | 6 | 2 | SC15 | 9 | 9 | 0 |
总延迟=18. 5 适应度值=0.05128 | |||
HC8 | 9 | 6 | 3 | HC1 | 10 | 9 | 1 | ||||
HC12 | 10 | 6 | 4 |
| |||||||
SC4 | 12 | 9 | 3 | ||||||||
SC10 | 13 | 9 | 4 | ||||||||
LC14 | 14 | 14 | 0 | ||||||||
LC11 | 15.5 | 14 | 1.5 | ||||||||
表10 适应值趋于平稳的机场航班染色体
HC2 | HC9 | HC5 | HC3 | HC13 | HC8 | SC4 | SC10 | HC12 | HC7 |
1 | 1 | 2 | 2 | 3 | 3 | 1 | 1 | 2 | 3 |
LC11 | LC14 | HC1 | LC6 | SC15 |
|
|
|
|
|
1 | 1 | 2 | 3 | 2 |
|
|
|
|
|
表11 飞机簇遗传算法仿真结果
1号跑道 | 2号跑道 | 3号跑道 | |||||||||
航班代号 | S | Emin | 延迟时间 | 航班代号 | S | Emin | 延迟时间 | 航班代号 | S | Emin | 延迟时间 |
HC2 | 6 | 6 | 0 | HC5 | 6 | 6 | 0 | HC13 | 6 | 6 | 0 |
HC9 | 7 | 7 | 0 | HC3 | 7 | 7 | 0 | HC8 | 7 | 7 | 0 |
SC4 | 9 | 9 | 0 | HC12 | 8 | 8 | 0 | HC7 | 8 | 8 | 0 |
SC10 | 10 | 9 | 1 | HC1 | 9 | 9 | 0 | LC6 | 13 | 13 | 0 |
LC11 | 14 | 14 | 0 | SC15 | 11 | 9 | 2 | 总延迟=4. 5 适应度值=0.1818 | |||
LC14 | 15.5 | 14 | 1.5 |
| |||||||
做出遗传算法排序得到的最大适应度值和平均适应度值进行曲线以及FCFS的适应度值,如图9所示。
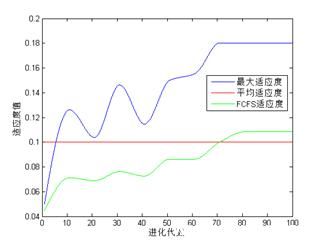
图9:历代适应度进行曲线
7.2.5 结果分析
采用自适性的遗传算法,经过70~80代遗传后,适应值趋于稳定状态。从遗传算法历代适应度进行曲线可以看出,经过多代遗传后,种群的适应度值区域一个稳定的值。遗传算法的总体趋势是提高染色体的适应度值,但计算过程中可能出现局部种群质量有所下降现象,但不影响曲线的整体上升趋势。
以先到先服务原则结果中以飞机航班![]() 为例,航班
为例,航班![]() 预计到达时间
预计到达时间![]() 为
为![]() ,按先到先服务原则排序到达时间为
,按先到先服务原则排序到达时间为![]() 为
为![]() ,航班
,航班![]() 会延迟
会延迟![]() 。
。
而在遗传算法结果中,比较飞机航班![]() 的延迟情况,预计达到时间
的延迟情况,预计达到时间![]() 为
为![]() ,遗传算法排序时间也为
,遗传算法排序时间也为![]() ,没有延迟。将机场飞机簇延迟时间累加,先到先服务原则飞机预计同时到达跑道时的总延迟时间为
,没有延迟。将机场飞机簇延迟时间累加,先到先服务原则飞机预计同时到达跑道时的总延迟时间为![]() ,遗传算法原则的总延迟时间为
,遗传算法原则的总延迟时间为![]() 。
。
比较先到先服务仿真结果和自适性遗传算法排序结果可以看出,将结果中机场飞机簇总延迟时间由先到先服务的18.5个时间单位减少到遗传算法原则的4.5个时间单位,延时减少了75.7%,适应度值由先到先服务的0.05128上升到遗传算法的0.1818,适应度值增加了254.5%。自适性遗传算法排序结果明显优于先到先服务的排序结果。并且通过飞机簇排序结果可以看出遗传算法倾向于将同类型的飞机组成同跑道的飞机簇。分析最小尾流标准可知,同类型飞机的最小尾流间隔最小,可以更优的缩短延迟时间,尽量避免由一时间段的飞机簇延误对下一时间段飞机簇的延误波及。
7.3 模型二的建立—机位分配健壮模型
7.3.1模型的准备
(1)航班延误分布规律
模型利用机场航班统计数据经过整理制作了基地航班公司(简称航空公司![]() )与非基地航班公司(简称航空公司
)与非基地航班公司(简称航空公司![]() )的航班到达延误分布。航空公司延误表示为相对于计划到港时间的偏离,
)的航班到达延误分布。航空公司延误表示为相对于计划到港时间的偏离,![]() 表示航班提前到达
表示航班提前到达![]() ,
,![]() 表示航班延误
表示航班延误![]() ,0表示航班按照航班计划准点到达。
,0表示航班按照航班计划准点到达。
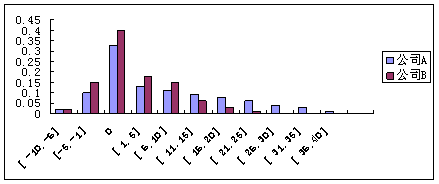
图10 航班到达延误分布
由图10可看出航空公司A、B在航班延误的时间分布范围和分布比例上都存在比较明显差异航空公司A航班最大延误为40min,而航空公司B航班最大延误只有25min.航空公司B准点到达概率为40%,而航空公司A只有33%。由航班到达延误分布图可以得到航空公司A、B航班到达延误分布概率,如表12所示。
表12 A、B航班到达延误分布概率
延迟时间\公司 公司A 公司B
[ -10,-6] 0.02 0.02
[ -5,-1] 0.10 0.15
0 0.33 0.40
[ 1,5] 0.13 0.18
[ 6,10] 0.11 0.15
[ 11.15] 0.09 0.06
延迟时间\公司 公司A 公司B
[ 16,20] 0.08 0.03
[ 21,25] 0.06 0.01
[ 26,30] 0.04 0.00
[ 31,35] 0.03 0.00
[ 36,40] 0.01 0.00
(2)机位冲突概率
被指派到统一机位的两个航班在多大程度上可能发生机位冲突,不但取决于这两个航班各自的延误概率分布。并且航空公司A的2个航班被指派到同一机位,和航空公司A、B的两个航班被指派到同一机位,即使指派到同一机位2个航班间的时间间隔相同,其发生机位冲突的可能性也会存在较大差异,如图11所示。
图11 航班冲突
(3)航班到港离港时间统计表:
表13 航班到港离港时间统计表
航班号计划到港时间 计划离港时间 航班号计划到港时间 计划离港时间
A22 9:00 11:40 A14 12:20 13:20
B18 9:11 10:00 A10 12:22 13:10
A35 9:12 10:12 B21 12:30 13:40
A50 9:12 10:10 A29 12:30 13:20
A11 9:24 10:40 A47 12:35 13:30
B 3 9:45 10:50 A41 12:40 13:25
A19 9:46 11:30 A60 12:48 13:35
A61 9:50 12:00 A51 12:55 13:50
A 5 10:08 10:55 A 2 13:10 14:00
A 4 10:10 12:00 A23 13:12 14:05
A34 10:10 11:00 A26 13:20 14:20
B 9 10:15 11:14 A32 13:22 14:15
B57 10:30 11:30 A44 13:26 14:20
A 1 10:35 11:28 A58 13:44 14:30
A20 11:00 12:00 B15 13:52 14:50
续表13
航班号计划到港时间 计划离港时间 航班号计划到港时间 计划离港时间
A25 11:00 12:15 A 8 14:00 14:55
A46 11:02 12:05 B 6 14:08 15:00
A28 11:05 12:10 A55 14:15 15:05
B54 11:10 12:12 A42 14:25 16:00
A 5 12:28 13:18 B52 14:32 15:30
A40 11:14 12:40 A24 14:40 15:50
B56 12:26 13:06 A 7 14:42 15:35
B45 11:30 12:31 A72 14:46 16:10
A49 13:40 14:35 A33 14:48 15:40
A62 11:40 12:42 B32 14:52 15:45
A37 11:45 12:45 A15 14:55 15:55
B12 11:48 12:50 B 5 14:58 15:50
7.3.2模型的建立
Ⅰ.模型参数定义
令![]() 分别为需要指派机位的航班数量和机场可用的机位数量;
分别为需要指派机位的航班数量和机场可用的机位数量;
![]() 、
、![]() 分别为航班
分别为航班![]() 的计划到港时间和计划离港时间;
的计划到港时间和计划离港时间;
![]() 为机位
为机位![]() 的开始可用时间;
的开始可用时间;
![]() 为机位
为机位![]() 的机位类型,
的机位类型,![]() 属于
属于![]() ;
;
![]() 为航班
为航班![]() 的类型,
的类型,![]() 属于
属于![]() ,当
,当![]() 时,航班
时,航班![]() 可停靠机位
可停靠机位![]() ;
;
![]() 为机位最短衔接时间,即前一个航班离开某机位到下一个航班到达该机位最短的安全时间间隔;
为机位最短衔接时间,即前一个航班离开某机位到下一个航班到达该机位最短的安全时间间隔;
![]() 为参照历史延误分布下航班j的最大提前到港时间,
为参照历史延误分布下航班j的最大提前到港时间,![]() ,
,![]() 分别为航空公司A、B航班的最大提前到港时间;
分别为航空公司A、B航班的最大提前到港时间;
![]() 为参考历史延误分布下的航班j的最大延误,
为参考历史延误分布下的航班j的最大延误,![]() ,
,![]() 分别为航空公司A,B航班的最大延误;
分别为航空公司A,B航班的最大延误;
![]() 为0-1决策变量,如果航班
为0-1决策变量,如果航班![]() 被指派到机位k,则
被指派到机位k,则![]() 为1,否则为0;
为1,否则为0;
![]() 为0-1决策变量,如果航班
为0-1决策变量,如果航班![]() 和航班j先后被指派到同一机位
和航班j先后被指派到同一机位![]() ,即
,即![]() ,则
,则![]() 为1,否则为0;
为1,否则为0;![]() 为航班
为航班![]() 在机位
在机位![]() 发生机位使用冲突的概率。
发生机位使用冲突的概率。
当航班![]() 先后被指派到同一机位
先后被指派到同一机位![]() ,即
,即![]() ,且这两个航班可能在某个时间段同时占用该机位,则航班
,且这两个航班可能在某个时间段同时占用该机位,则航班![]() 在机位
在机位![]() 发生机位使用冲突的概率
发生机位使用冲突的概率![]() 为
为
![]() (16)
(16)
式中:![]() 分别为航班
分别为航班![]() 和航班j在时间范围
和航班j在时间范围![]() 内占用机位k的概率。
内占用机位k的概率。
Ⅱ.数学模型
以总的航班机位冲突概率Z最小为目标函数,以机位与航班类型为约束条件,建立模型为:
 目标函数式(17)表示所有被指派到同一机位的两个航班发生机位冲突概率最小;式(18)表示一个航班智能分配给以个机位;式(19)表示航班类型要与机位类型相匹配;式(20)用于判断两个航班是否被指配到同一机位;式(21)表示分配到同意机位的前后2个航班,其离港和到港时间应满足最短的安全衔接时间要求。
目标函数式(17)表示所有被指派到同一机位的两个航班发生机位冲突概率最小;式(18)表示一个航班智能分配给以个机位;式(19)表示航班类型要与机位类型相匹配;式(20)用于判断两个航班是否被指配到同一机位;式(21)表示分配到同意机位的前后2个航班,其离港和到港时间应满足最短的安全衔接时间要求。
Ⅲ.算法设计
由于航班的到达延误呈现离散分布,与传统机位指派问题中的旅客步行距离、飞机滑行距离、航班等待等指标相比,机位冲突概率的取得相对较难,普通的线性规划方法并不适合本文建立的模型。启发式算法是解决优化问题比较有效的方法,本文设计了贪婪禁忌搜索算法[3]求解问题。
贪婪算法步骤
Step 1:将所有航班按计划到港时间![]() 的先后顺序进行排序,产生1个航班计划到计划到港时间的队列。
的先后顺序进行排序,产生1个航班计划到计划到港时间的队列。
Step 2:从上述航班队列中当前第一个航班开始,从现有机位中选择机位可用时间![]() 的备选机位集合,即航班到港后可供其选择停靠的机位集合。
的备选机位集合,即航班到港后可供其选择停靠的机位集合。
Step 3:在备选机位集合中计算所有元素的目标函数值,选择目标函数值最小的机位![]() 作为当前航班指派的机位。
作为当前航班指派的机位。
Step 4:更新被指派机位![]() 的最早可用时间,在航班序列中去除第一个航班。
的最早可用时间,在航班序列中去除第一个航班。
Step 5:如果航班序列为空,则输出指派结果,否则转Step 3.
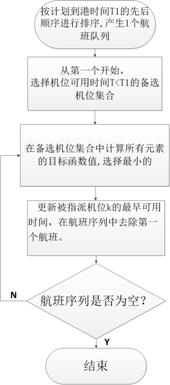
图12 贪婪算法流程图
贪婪算法只是实现了在每个指派时间点上目标函数的最优,属于局部优化,需要进一步通过禁忌搜索的方法进行全局优化
禁忌搜索算法步骤
Step 1:初值设定。使用贪婪算法生成的初始解![]() ,令当前解
,令当前解![]() ,初始化禁忌条件,另禁忌搜索迭代次数计数变量的初始值为0.
,初始化禁忌条件,另禁忌搜索迭代次数计数变量的初始值为0.
Step 2:终止条件。本文将禁忌搜索的最大迭代次数设定为100,并将其作为算法的终止条件,如果算法运行到设定的最大迭代次数,则终止程序,记录并输出最优解Z2,否则转Step3.
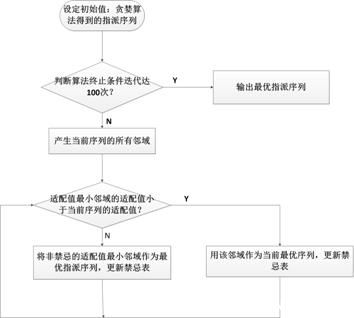
图13 禁忌搜索流程图
Step 3:邻域搜索。产生当前解![]() 的所有邻域解,对于
的所有邻域解,对于![]() 个航班需要指派到
个航班需要指派到![]() 个机位的机位指派问题,向量
个机位的机位指派问题,向量![]() 构成机位指派问题的一个解,如果向量
构成机位指派问题的一个解,如果向量![]() 与向量
与向量![]() 的对应元素至少有一个元素不相同,则称
的对应元素至少有一个元素不相同,则称![]() 是
是![]() 的领域。本文使用插入移动和交换移动的方法,构成当前解的所有邻域解。
的领域。本文使用插入移动和交换移动的方法,构成当前解的所有邻域解。
Step 4: 藐视准则。计算当前解Z1所有邻域解对应的适配值,记录适配值最小的邻域![]() ,本文直接把目标函数作为适配值函数。如果Z3对应的适配值小于当前最优解
,本文直接把目标函数作为适配值函数。如果Z3对应的适配值小于当前最优解![]() 对应的适配值,则令
对应的适配值,则令![]() (藐视准则),将
(藐视准则),将![]() 与
与![]() 交换,作为禁忌对象替换最早进入禁忌表的禁忌对象,转Step 6否则,继续Step 5.
交换,作为禁忌对象替换最早进入禁忌表的禁忌对象,转Step 6否则,继续Step 5.
Step 5:分散搜索。判断邻域解对应的各对象的禁忌属性,在候选解集非禁忌对象中选取使得最小的邻域解作为![]() ,令
,令![]() ,同时将
,同时将![]() 与
与![]() 交换,作为禁忌对象替换最早进入禁忌表的禁忌对象。
交换,作为禁忌对象替换最早进入禁忌表的禁忌对象。
Step 6:更新迭代次数,转至 Step2.
7.3.3模型结果
冲突概率计算结果如表14所示。
表14 航班冲突概率结果
贪婪指派 | 禁忌搜索 | ||||
机位号 | 停靠航班 | 冲突概率 | 停靠航班 | 冲突概率 |
|
101 | A22、A14、A58 | 0.0873 | A22、A14、A58 | 0.0873 | 0 |
102 | B18 B57 B12 A26 | 0.1876 | B18 B57 B12 A26 B32 | 0.2212 | -0.0336 |
103 | A35 A1 A37 A23 | 0.1924 | A35 A1 A37 A23 | 0.1924 | 0 |
104 | A50 A20 A10 A58 | 0.2103 | A50 A20 A10 A58 | 0.2103 | 0 |
105 | A11 A25 A47 B15 | 0.1872 | A11 A25 A47 B15 | 0.1872 | 0 |
106 | B3 B54 A41 A8 | 0.1764 | A61 B21 B6 A24 | 0.1726 | 0.0038 |
107 | A19 A37 A2 A42 | 0.1988 | A19 A37 A2 A42 | 0.1988 | 0 |
108 | A61 B21 B6 | 0.0865 | B3 B54 A41 A8 | 0.0983 | -0.0118 |
109 | A53 A40 A51 A55 | 0.2214 | A53 A40 A51 A55 | 0.2214 | 0 |
110 | A4 A29 B52 | 0.0954 | A4 A29 B52 | 0.0954 | 0 |
111 | A34 A62 A60 A24 | 0.1892 | A34 A62 A60 | 0.1026 | 0.0866 |
112 | B9 B45 A32 | 0.0764 | B9 B45 A32 A15 | 0.1072 | -0.0308 |
113 | A46 B56 A44 A15 | 0.1758 | A46 B56 A44 | 0.0885 | 0.0873 |
114 | A28 A5 A49 B32 | 0.1642 | A28 A5 A49 | 0.0923 | 0.0719 |
总计 |
| 2.2489 |
| 2.0755 | 0.1734 |
7.3.4结果分析
模型研究了航空公司![]() 在典型日
在典型日![]() 的部分到港航班数据,共
的部分到港航班数据,共![]() 航班,
航班,![]() 个可用机位。在航空公司
个可用机位。在航空公司![]() 航班到达时间符合历史航班延误分布历史规律时使用贪婪算法和禁忌搜索优化冲突概率。以上表机位
航班到达时间符合历史航班延误分布历史规律时使用贪婪算法和禁忌搜索优化冲突概率。以上表机位![]() 为例分析,贪婪指派后机位
为例分析,贪婪指派后机位![]() 停靠航班为A28、A5、A49、B32,此机位冲突概率为0.1642,经过禁忌搜索最优后机位
停靠航班为A28、A5、A49、B32,此机位冲突概率为0.1642,经过禁忌搜索最优后机位![]() 停靠航班为A28、A5、A49,此机位冲突概率为0.0923,经过优化后机位冲突概率减少了0.0719。
停靠航班为A28、A5、A49,此机位冲突概率为0.0923,经过优化后机位冲突概率减少了0.0719。
从冲突概率计算结果可以看出,通过贪婪算法得到的初始指派方案机位冲突的概率总和为2.2489,经过禁忌搜索优化,在所有14个机位中,共有7个机位上的航班初始指派方案得到了交换移动,虽然102,108,112在禁忌搜索之后目标值略有增加,但却使得机位106,111,113和114的目标值得到了更大程度的改善,体现出了全局优化的优势,最终使得指派方案的机位冲突概率降到了2.0755,冲突概率的改进值0.1734,为即通过禁忌搜索计算可以进一步提高解的质量,分析可知贪婪禁忌搜索算法更注重于机位冲突概率的大小,包含了对航班时间间隔和航班延误概率分布的同时考量。
7.4 灵敏度分析
表15 贪婪禁忌搜索、遗传算法灵敏度比较
算法 达到最优解运行次数 运行时间 初始值 最优解
贪婪禁忌算法 35 1.20 2.7647 2.7371
遗传算法 78 37.52 3.1243 2.7412
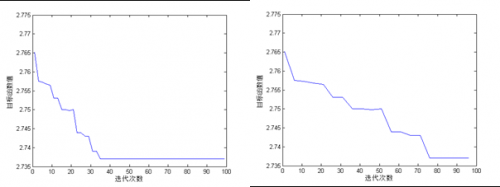
针对模型四机位分配健壮模型,通过与遗传算法对比可以发现贪婪禁忌搜索算法在实现最优解的运行时间、运算次数和初始解质量上比遗传算法具有较高的优越性,两种算法的最优解也比较接近,但是禁忌搜索算的最优解仍然相对较优具体比较结果见表15。
图14 禁忌搜索算法迭代图 图15 遗传算法迭代图
分析形成差异的主要原因是在于初始解的获得方法上,传统遗传算法使用随机方法获得第1代种群,所以最优解的搜索空间相对较大,通过基因交叉、变异实现染色体进化的过程相对较长,运行时间也相对较长。而禁忌搜索算法通过贪婪算法获取初始可行解,在一定程度上缩小了最优解的搜索空间。具体比较结果见图14和图15。
八.模型优缺点
8.1.优点
(1)模型一使用了基于改进的AHP的指标权重确定方法,通过聚类的思想最大程度上减小了机构打分主观因素对整个体系评分的影响。
(2)因为影响航班延误的因素很多,所以模型二运用主成分回归模型,将比较多的因素用PCA以后找到三个主成分,并用三个主成分建立最小二乘模型,更加客观体现出影响航班延误的主要因素。
(3)在分析解决航班延误问题中,我们使用了自适应遗传算法,加快了程序运行速度。
(4) 与现有方法相比,使用机位分配健壮模型是机位计划鲁棒性提高,准确反映机位冲突可能。机位分配健壮模型没有考虑航班到达机场后机场由于场地地面原因引起的二次延误,在遗传算法终端排队模型中得以解决.
8.2.缺点
(1)在模型一中,因为机构打分项较少,所以筛选以后对整体的排名影响不大。
(2)用主成分分析出三个主成分,但是对主成分的解释并不是特别合理。
8.3模型推广
(1)本模型不仅可以用用于终端区多条跑道多架飞机排序中的跑道分配和飞机排序,还可以应用于多架飞机在相同时间起飞时的排序问题。
(2)可以推广到不同机场中具有延时分布差异化的不同航空公司进行冲突概率最小化。
九.参考文献
[1] 双同科,田佳林.一种基于改进AHP的指标权重确定方法[J].中国西部科技.2011(10):37-38.
[2] 机场航班.美国航空数据[EB/OL].http://www.flightstats.com/go/Home/home.do
[3] 李军会 ,朱金福等基于航班延误分布的机位鲁棒指派模型[J].交通运输工程学报.2014(6):75-82.
[4] 姜启源,谢金新.数学模型[M].4版.北京:高等教育出版社,2014.
[5] 徐肖豪 ,姚源.遗传算法在终端区飞机排序中的应用[J].交通运输工程学报.2004,4(3):121-126.
[6] 中国民用航空局发展计划司.从统计看民航[M].北京:中国民航出版社,2010.
[7] 中国民用航空局发展计划司.从统计看民航[M].北京:中国民航出版社,2011.
[8] 中国民用航空局发展计划司.从统计看民航[M].北京:中国民航出版社,2012.
[9] 中国民用航空局发展计划司.从统计看民航[M].北京:中国民航出版社,2013.
[10] 胡虎肇.基于主成分回归模型的福建省农民增收因素分析[J].台湾农业探索.2010(2):50-52.